弹性因子研究
【摘要】
近几年来,随着传统多因子模型在市场的应用逐渐广泛,因子的波动特征逐渐加大,因子拥挤等原因造成了因子的收益逐渐下降。为了能够寻找更好的Alpha收益来源,在多因子模型框架中,因子作为底层Alpha来源输入的基础,因子的开发、迭代、更新就显得越来越重要。
深度和广度作为表征流动性维度的两大类已被广泛探讨。然而,弹性作为流动性维度的另一面尚缺乏相关研究。本专题研究探讨了流动性股票市场的弹性测量,并明确构建出弹性因子,研究其在因子选股中的应用。
一、深度、广度、弹性根据Bernstein (1987) ,深度、广度和弹性是流动性股票市场的基本要素。在这些要素中,深度和广度作为表征流动性维度的两大类已被广泛研究:一方面是交易活动,如总交易量或股票换手率,代表市场投资者如何积极交易资产。另一面是交易成本,通常通过 Amihud (2002) 的非流动性度量或买卖价差度量来估计,以捕捉投资者在执行市场订单时应承受的价格影响水平。关于这两大类的流动性度量已在大量文献中有明确的定义。然而,流动性维度的另一面,即弹性,相关研究较为稀少。
弹性的概念早在之前的几项研究中被引入。Black (1971) 将流动性市场描述为一个持续且有效的市场。在该市场中,可以以非常接近当前价格的价格立即买卖证券。
Kyle (1985) 提到弹性是价格从无信息的随机冲击中恢复的速度。Bernstein (1987) 从秩序失衡的角度解释弹性。他认为,弹性意味着大量订单流抵消了由于临时订单不平衡而导致的交易价格变化。
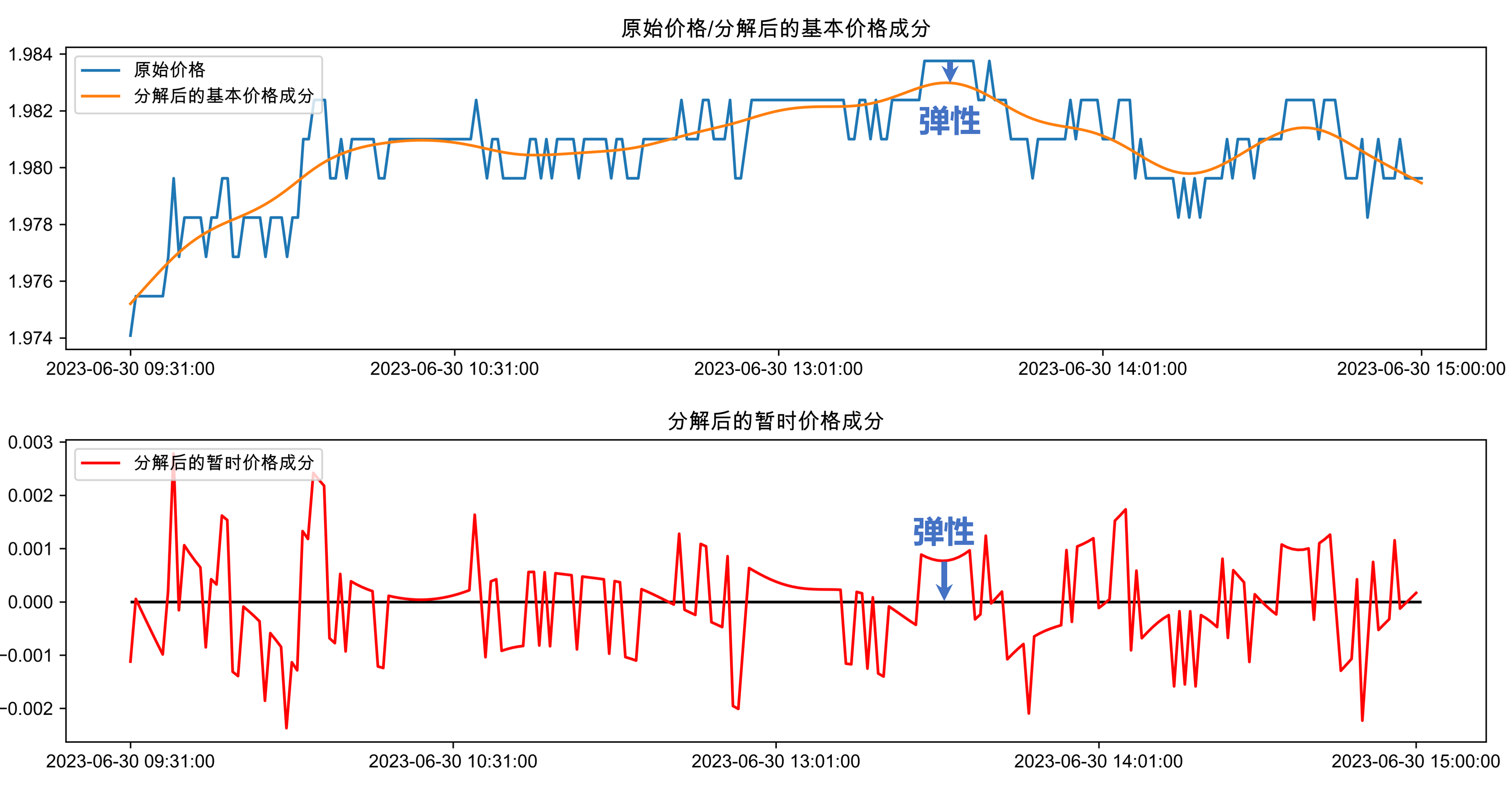
Harris (2003) 明确指出,弹性是指价格在响应流动性需求者或没有信息优势交易者发起的大量订单流失衡而发生变化后,价格恢复到价值交易者驱动的基本价值的速度。在这方面,弹性可以描述为价格从信息优势交易者驱动的先前暂时价格影响恢复到其基本价格的速度。
基于以上定义,本报告研究测量弹性并构建出弹性因子,度量其能否在股票市场中获得超额收益。为了计算出弹性水平并构建弹性因子,本文参考Jinyong Kim等人在2015年发表的学术论文《Transitory Price, Resiliency, and the Cross-Section of Stock Returns》,首先将每日股价分解为基本成分和暂时成分。在完成股价分解后,将估计的每日暂时价格序列转换为频域中的频谱函数形式,并计算出暂时价格恢复的速度作为弹性因子。
二、弹性因子相关工作
现有研究对弹性的测量可以分为两大类。第一类是将弹性代表为股票价格的均值回归,这种方法主要关注股价本身的变动。Dong等(2007) 将弹性定义为股票在t-1和t期间的日内定价误差过程的均值回归参数。实证结果表明公司的预期股票回报与弹性呈负相关。
Anand等(2013) 建议用金融危机期间和之后交易成本相对于危机前时期超过two-sigma阈值的月份的平均百分比来衡量非弹性。实证结果表明,买方机构的流动性供应是后危机时期从流动性冲击中复苏的主要因素。 Kempf等(2015) 也使用交易成本度量来计算弹性。
Alan等(2015) 将弹性计算为开盘半小时股票收益与剩余交易日股票收益的日内序列相关性。通过公司层面和投资组合层面的分析,发现弹性与股票收益的横截面呈负相关。另一种类型的弹性测量侧重于交易成本测量方面的恢复过程,例如买卖价差或市场深度。
类似于Dong等(2007),Kempf等(2015) 使用盘中数据将弹性定义为先前交易成本水平和当前交易成本流的均值回归参数。
区别于上述相关研究,本报告定义的弹性测量直接衡量了暂时价格的恢复速度。 通过频域的频谱分析得到暂时价格的距离和恢复时间,然后用距离除以恢复时间来计算速度。因此,本文对弹性的测量更符合弹性的字面定义。
此外,本文的弹性测量被建模以克服Anand等(2013) 提出的问题,即现有研究仅考察短期内的弹性。 对此,本文对暂时价格变动进行建模时,使用了窗口期较长的过往数据,并考虑了其中多个频率成分的综合情况,以同时捕捉到长期复苏运动和短期复苏运动的速度。
三、弹性因子的构建方法如前文所述,股票价格可以分解为两个部分: 一个是永久性或随机游走成分,代表股票的基本价格随信息冲击而变化;另一个是暂时的或固定的组成部分,其中包含偏离其基本价值的暂时价格变动。
如上所述,弹性表示股票价格从短暂的价格影响中恢复到其基本价格的速度。在这方面,本文衡量的是暂时价格成分恢复到其基本价格的平均速度。更具体地说,为了度量股票的弹性并构建弹性因子,本文的构建方法分为以下两步程序:首先,将个股价格分解为基本价格和暂时价格。然后,使用频域中的频谱分析来计算暂时价格的恢复速度。此过程在以下部分中描述。
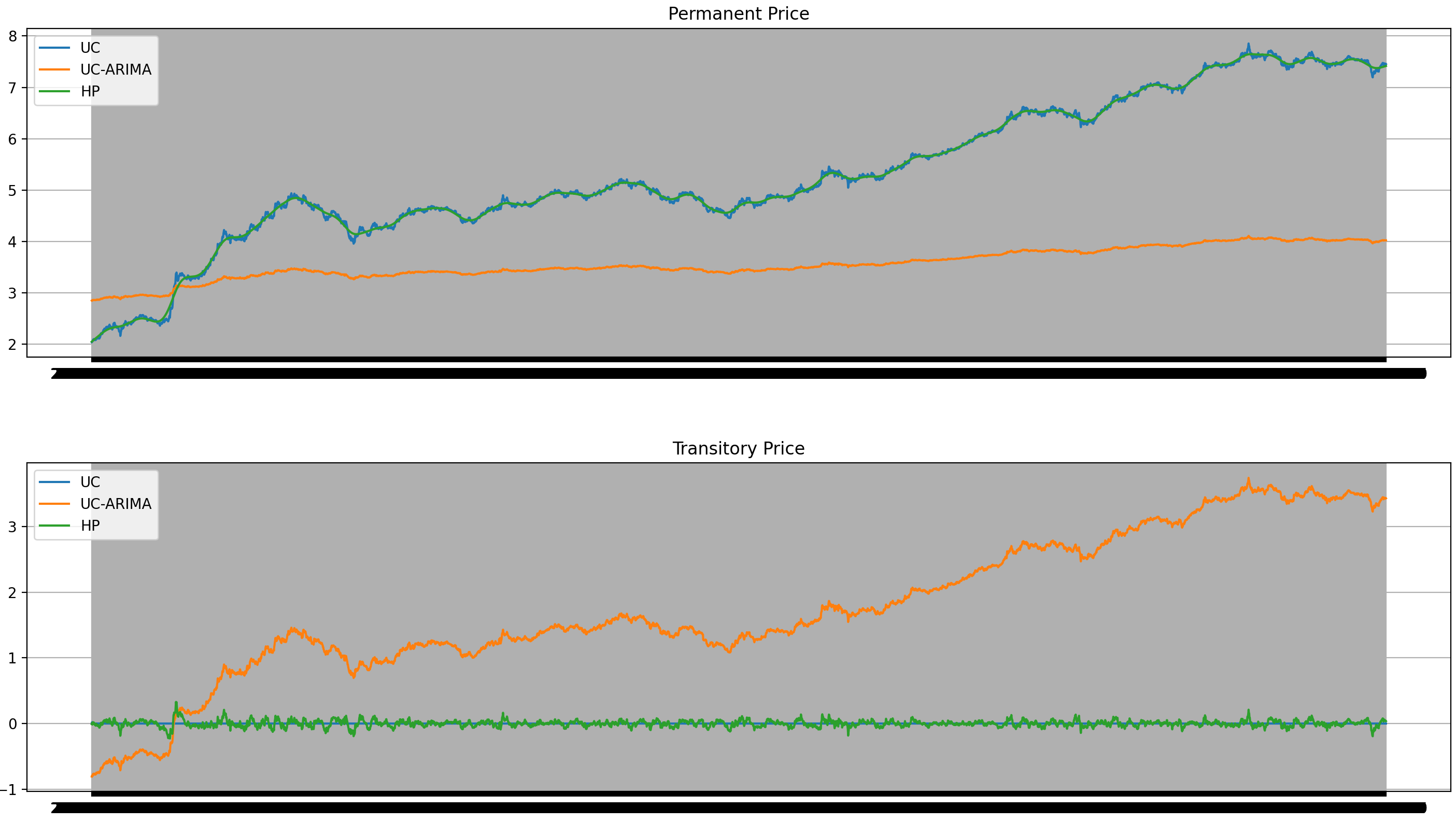
3.1 股票价格分解为了将单个股票价格在时间t的自然对数 \(p_t\) 分解为基本价格 \(q_t\) 和暂时价格 \(z_t\),本文考虑了三种在经济学数据分析中常用的分解算法:Hodrick-Prescott (HP),Unobserved components and ARIMA model (UC-ARIMA)和Unobserved components with stochastic cycle (UC)。
在理想状态下,基本价格应该体现为股票真实价格长期变动趋势的平滑曲线;而暂时价格则体现为围绕基本价格变动的跳跃,其在坐标轴上应为围绕0上下波动的曲线。
以下图为某股票从2005年1月至2022年12月的股价分解作为例子,HP算法分解结果中的基本价格最为平滑且能体现出其真实价格的长期变动趋势,同时暂时价格部分也最能体现波动。因此,本文采用HP算法,将取自然对数后的股票价格分解为基本价格和暂时价格。
3.2 弹性测量
具有更高回归速度的股票表明它可以更快地从先前的短暂价格影响中恢复过来。因此,投资者认为这只股票更具弹性,因而更具流动性。换句话说,暂时价格回归较慢的股票被视为风险较高的资产,需要向投资者补偿较高的风险溢价。
为了衡量恢复速度,本篇专题报告使用傅立叶变换将分解后的暂时价格序列转换为频域中的频谱函数形式。回归速度快的股票,其频谱函数主要分布在较高的频率水平,而回归速度慢的股票,其频谱函数主要分布在较低的频率水平。
在这里假设暂时价格序列是一个有限信号,它包含一个以上的频率成分,恢复到其基本价格。有限时间序列在时域和频域之间具有以下离散傅立叶变换关系,\(Z_k = \sum^{D}_{t=1}(z_te^{-\frac{i2\pi kt}{D}}), k = 1,2,...,D\)。
其中 \(z_t\) 为分解后的有限暂时价格序列,\(z_k\) 是 \(z_t\) 进行离散傅立叶变换后的频谱函数,\(k\) 是频域单位,\(D\) 是交易日总天数,\(i\) 是虚数单位。为了在不受交易日总天数影响的情况下估计频谱函数的纯幅度,使用 \(D\) 对 \(z_k\) 进行归一化,然后得到归一化函数形式 \(\overline{Z}_k\)。其中,\(\overline{Z}_k = \frac{1}{D}Z_k\), 并进一步计算得到归一化后的频谱函数的幅度 \(|\overline{Z}_k |\)。
由于频率被定义为每单位时间的周期数,因此周期 \(T_k = \frac{D}{k}\) 可以表示为频率分量的缩放版本的倒数 \(f_k = \frac{k}{D}\)。
幅度 \(|\overline{Z}_k |\) 表示在每个频率水平上偏离其基本值的短暂价格波动峰值的距离。周期 \(T\)捕获每个恢复摆动的周期完成的速度。因此,可以通过将 \(|\overline{Z}_k |\) 除以其对应的周期来获得每个频率级别的暂时价格的移动速度。
综上所述,暂时价格恢复的平均速度,即弹性因子的构建,可以通过以下等式计算获得:
\[\begin{align*} Resiliency_{i, t} & = \frac{1}{[\frac{D_{i, t}}{2}]} \sum^{[\frac{D_{i, t}}{2}]}_{k=1} \frac{2|\overline{Z}_{k, i, t}|}{T_{k, i, t}} \\ & = \frac{1}{[\frac{D_{i, t}}{2}]} \sum^{[\frac{D_{i, t}}{2}]}_{k=1} 2|\overline{Z}_{k, i, t}| f_{k, i, t} \end{align*}\]其中 \(D_{i,t}\) 是每个月 \(t\) 的滚动窗口中股票 \(i\) 的数据可用的样本天数,\([\frac{D_{i, t}}{2}]\) 是最接近 \(\frac{D_{i, t}}{2}\) 的整数。
为了构建弹性因子,在每月月末调仓时,针对每个个股,使用自2005年1月起至该调仓日所有可用的过去股价数据进行HP分解,得到基本价格和暂时价格,然后以36个月的滚动窗口通过离散傅立叶变换进行逐月计算得出每个个股的弹性水平。
四、弹性因子回测数据说明- 选股范围:全市场,创业板,沪深300,中证500,中证800,中证1000
- 股票预处理:剔除非上市、摘牌、ST/*ST、涨跌停板、上市未满1年股票
- 因子预处理:MAD去极值、Z-Score标准化、行业市值中性化
- 回测区间: 2010.01.01 - 2022.12.31(中证1000为2014.10.31 - 2022.12.31,创业板为2012.12.31 - 2022.12.31)
- 分档方式:根据当期股票因子值,从小到大分为五档
- 调仓周期:每个月最后一个交易日以收盘价调仓
- 交易费用:千分之三(卖出时收取)
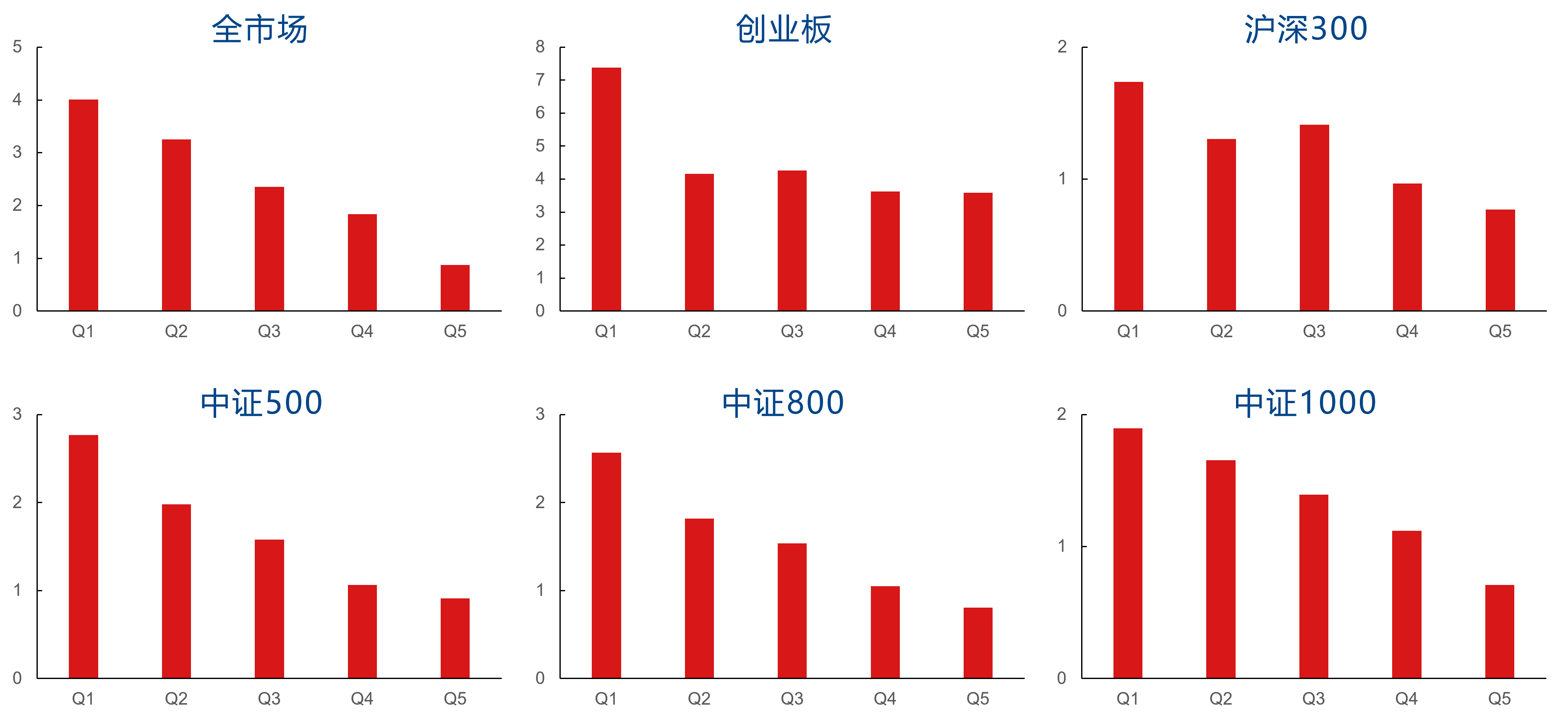
五、弹性因子回测表现
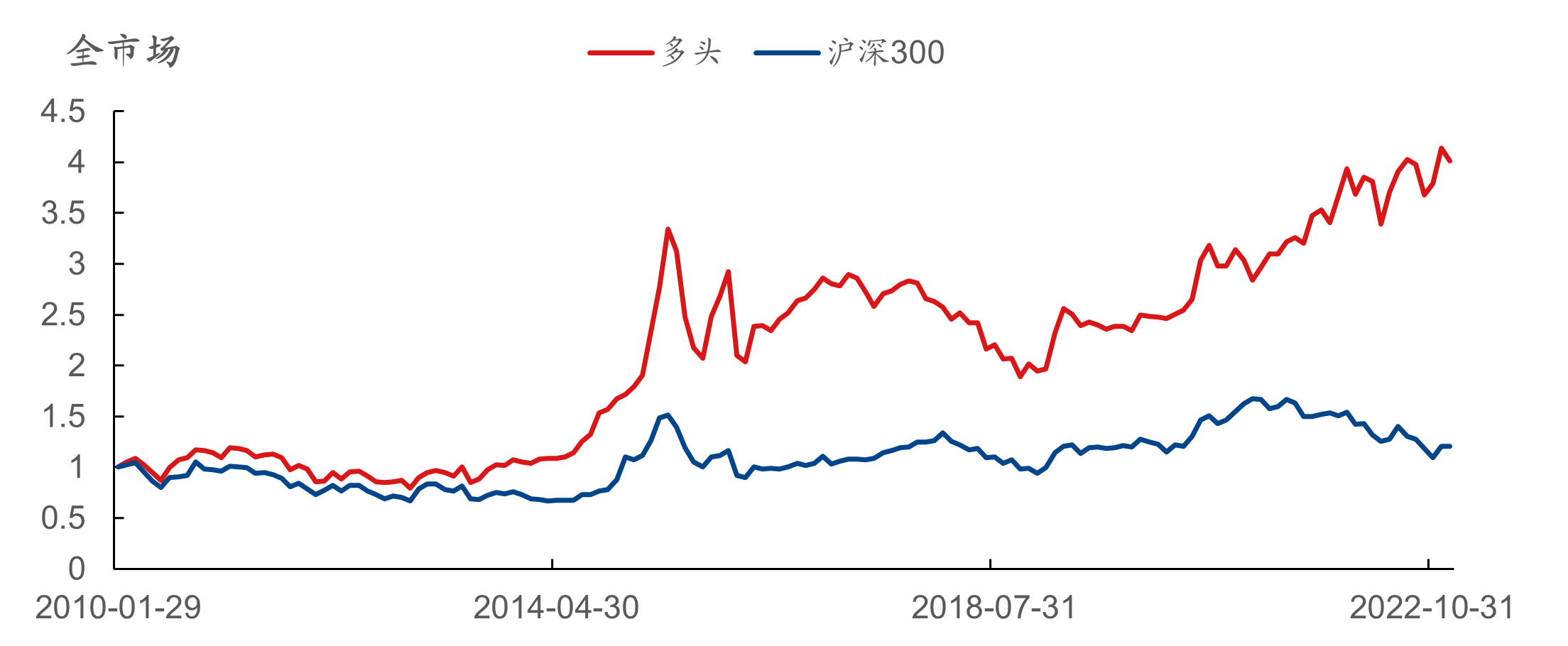
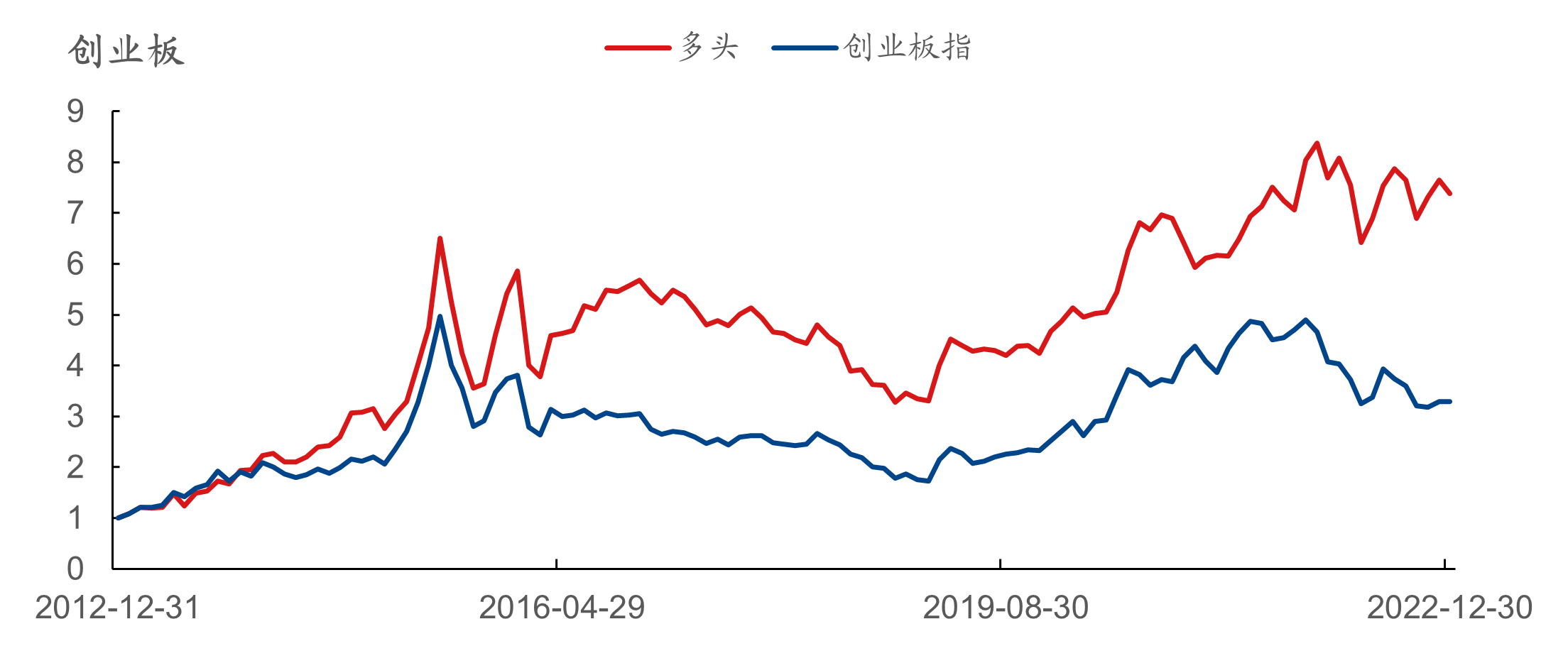
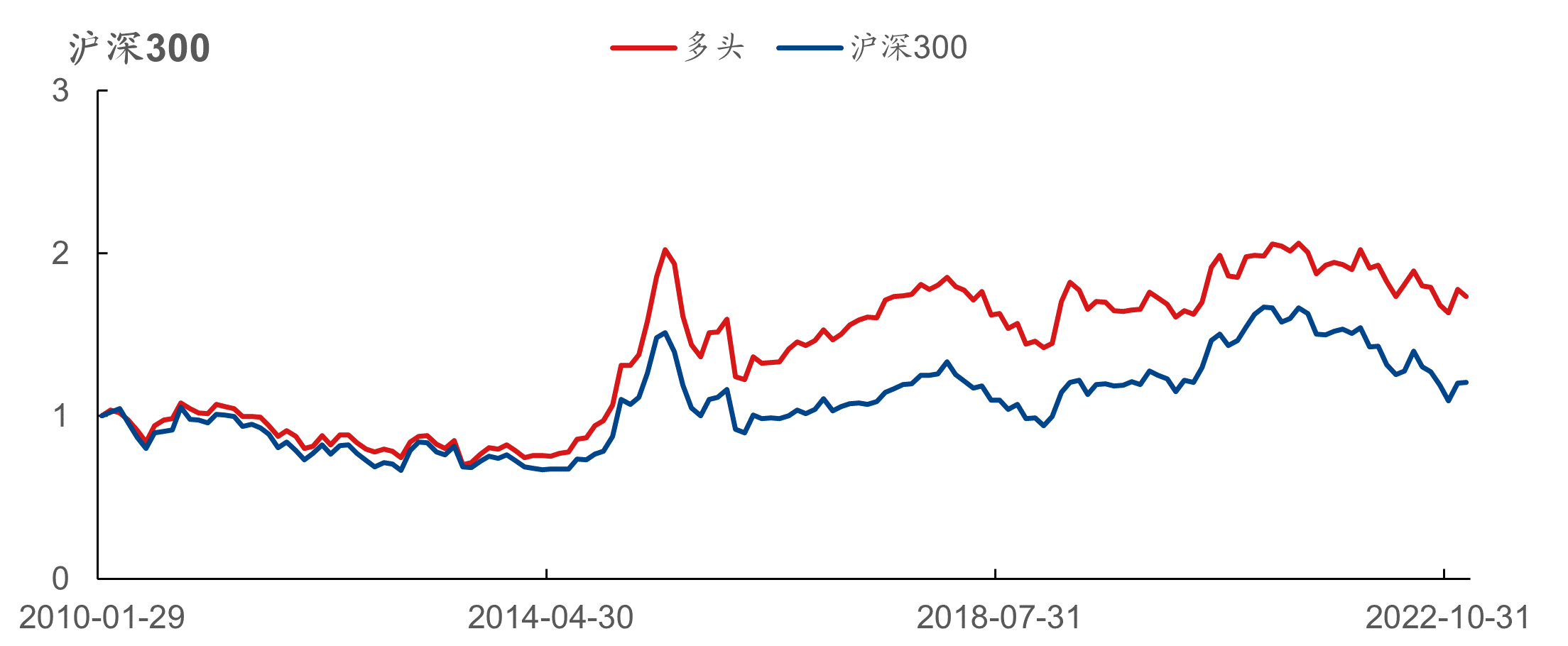
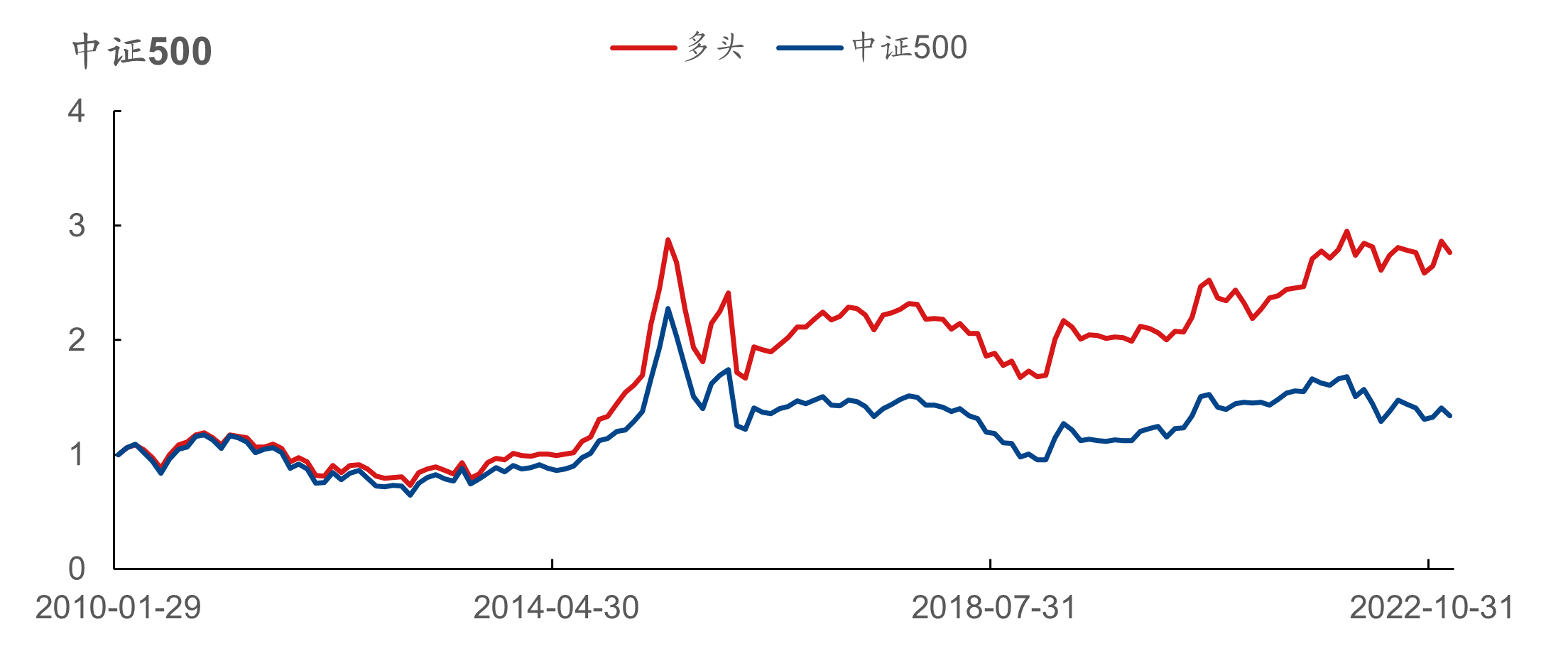
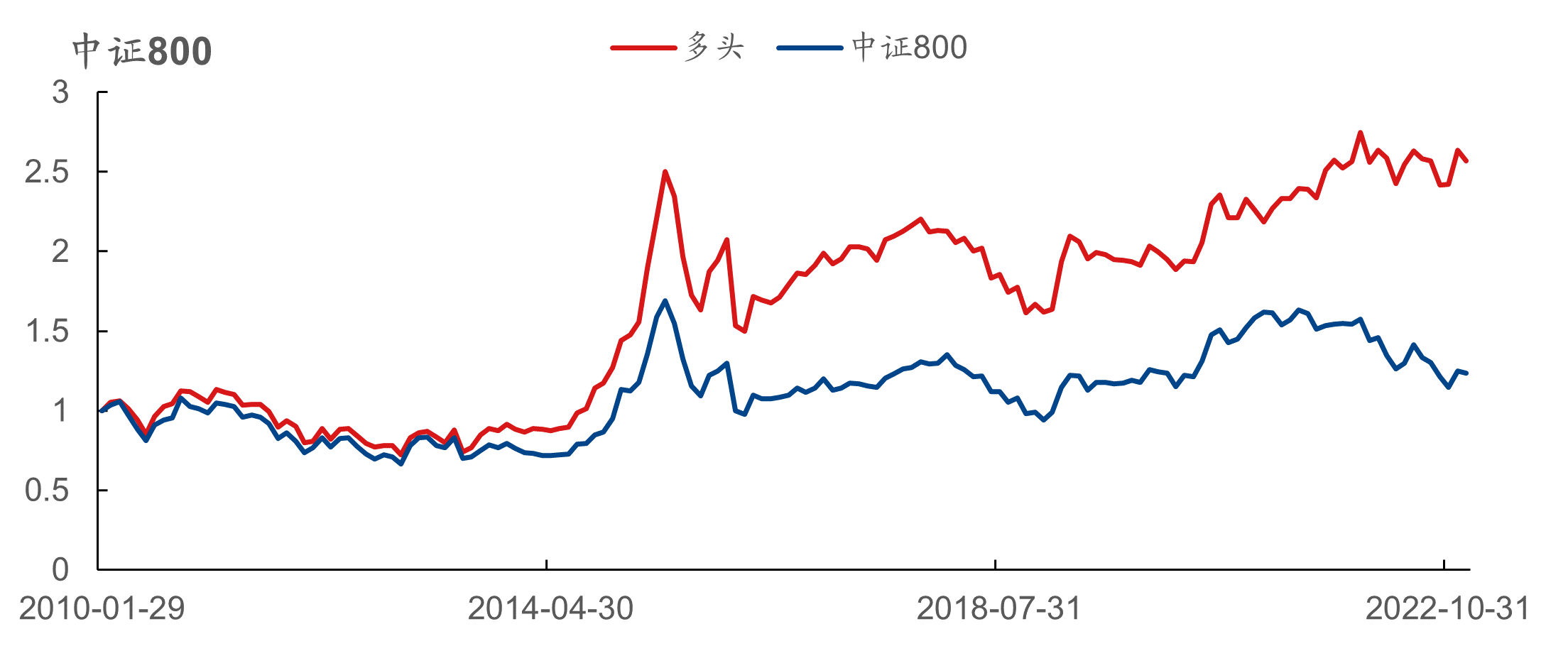
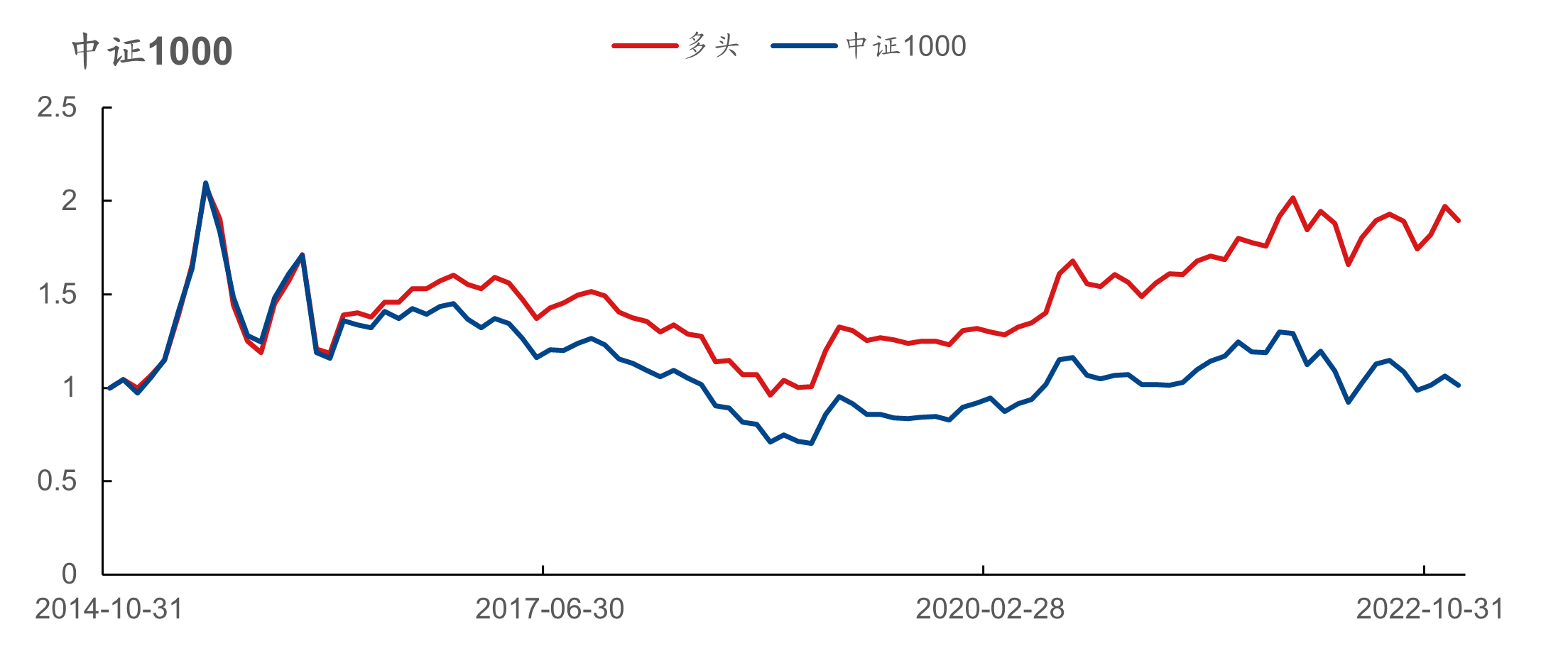
弹性因子的分档及历史累计收益表现如下图所示,在全市场、创业板、沪深300、中证500、中证800、中证1000板块中的RankIC均值分别为 -5.44%、 -4.18%、 -3.92%、 -4.58%、 -4.44%、 -6.27%,多头分别对应板块指数获得了9.87%、 9.48%、 2.88%、 5.91%、 5.92%、 8.01%的超额年化收益率。
六、总结
本研究探讨了流动性股票市场的弹性测量,并构建出弹性弹性因子,研究其在因子选股中的应用。实证分析结果表明,弹性因子在A股市场中具有不错的选股能力。
本研究以月频调仓对弹性因子在全市场、沪深300、中证500、中证800和中证1000板块的选股表现进行了实证分析。实证分析结果表明,弹性因子在各板块的分档效果均较为显著。
从具体收益来看,弹性因子在创业板的表现较为突出,在2013年1月至2022年12月期间多头年化收益率达22.12%,同期创业板指数年化收益率为12.64%,超额年化收益率达9.48%。
在中证1000板块,弹性因子多头年化收益率为8.15%,同期中证1000指数年化收益率为0.14%,具有较为明显的超额收益。
此外,弹性因子在全市场、沪深300、中证500、中证800的多头年化收益率分别为11.35%、4.36%、8.20%和7.58%。
参考文献(部分)
[1] Kim J, Kim Y. Transitory prices, resiliency, and the cross-section of stock returns[J]. International Review of Financial Analysis, 2019, 63: 243-256.
[2] Bernstein, P.L., 1987, Liquidity, stock markets, and market makers. Financial Management, 16(2), 54-62.
[3] Amihud, Y., 2002, Illiquidity and stock returns: cross-section and times-series effects, Journal of Financial Markets 5, 31-56.
[4] Black.F., 1971, Toward a fully automated stock exchange, Part 1. Financial Analysts journal, 27(4), 29-34.
[5] Kyle, A., 1985, Continous auctions and insider trading. Econometrica 53, 1315-1335.
[6] Bernstein, P.L., 1987, Liquidity, stock markets, and market makers. Financial Management, 16(2), 54-62.
[7] Harris, L, 2003, Trading & exchanges: Market microstructure for practitioner. Oxford University Press.
[8] Dong, J, A. Kempf, and P.K. Yadav, 2007, Resiliency, the neglected dimension of market liquidity: Empirical evidence from the New York Stock Exchange, Working Paper.
[9] Alan, N.S., J. Hua, L. Peng, and R.A. Schwartz, 2015, Stock resiliency and expected returns, Working Paper, version April 2015.
[10] Anand, A., P. Irvine, A. Puckett and K. Venkataraman, 2013, Institutional trading and stock resiliency: Evidence from the 2007-2009 financial crisis, Journal of Financial Economics 108, 773-797.
[11] Kempf, A., D. Mayston, M. Gehde-Trapp and P. K. Yadav, 2015, Resiliency: A dynamic view of liquidity, Working Paper.