From Coarse to Fine:从多日到日内的订单拆分策略——从流动性角度出发
【摘要】
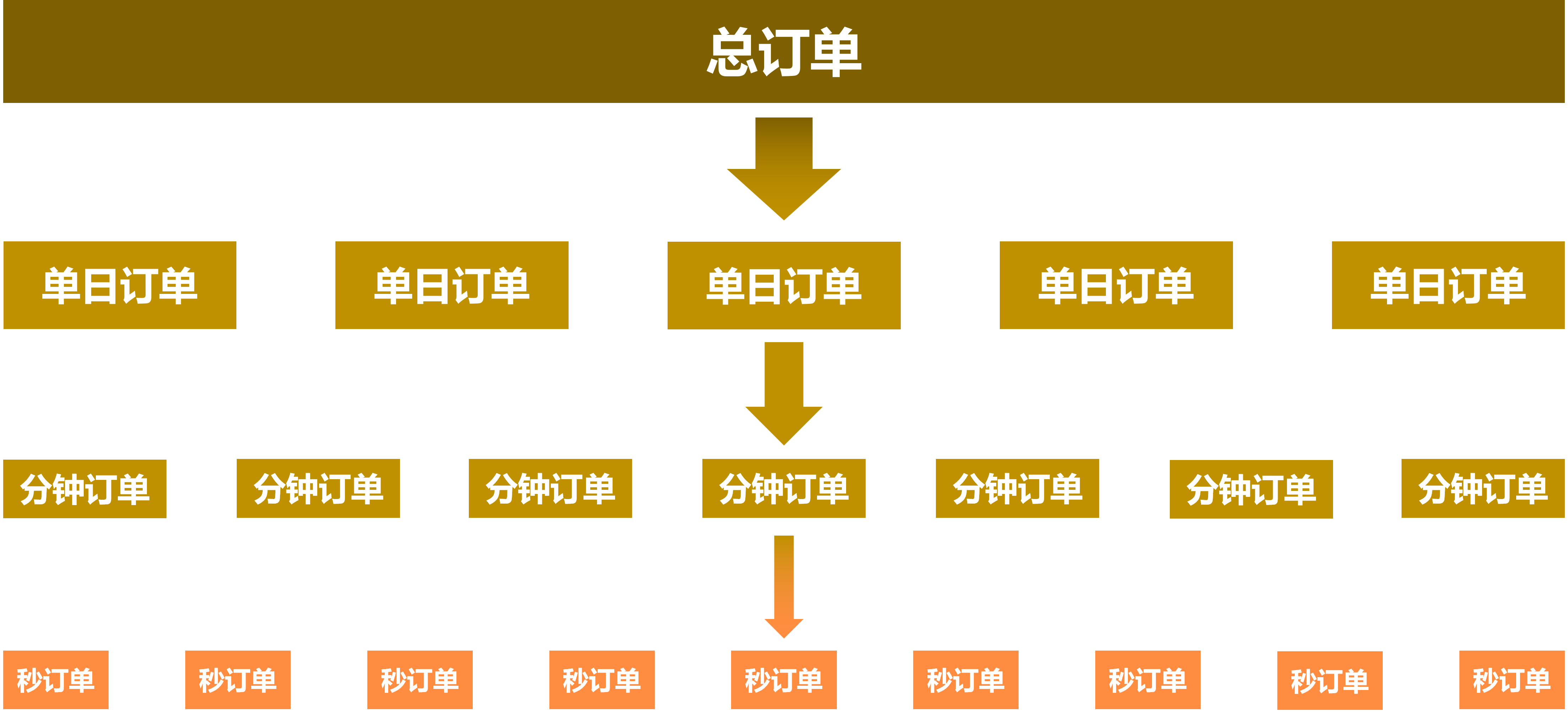
本研究采用“从粗到细”的思路构建订单拆分策略,旨在降低大额成交需求所产生的冲击成本。通过综合考虑股票的“流动性+股价”,在“价和量”之间找到最佳平衡点,实现交易成本的全局最优。
具体而言,本研究的订单拆分策略分为两部分。第一部分首先采用流动性因子对标的股票的未来流动性走势进行判断,并结合本研究所提出的二元概率预测多日订单拆分算法,把一个大额订单拆分为多个单日订单;第二部分提出了采用基于冲击成本分布统计的日内订单拆分算法,进一步把单日订单拆分为分钟级甚至是秒级的微小订单,以此来达到降低冲击成本的目的。
一、股票流动性
股票的流动性越好,则其冲击成本越低。因此,若想降低大额订单的因冲击成本所导致的交易成本,则应该对其进行拆分,在流动性高的时候交易更多的份额,而在流动性低的时候交易更少的份额。在本研究中,采用4个因子对股票的流动性进行综合衡量
1.1 冲击成本因子在订单驱动市场中,市场的流动性是由交易者的限价订单提供的。本研究参考上海证券交易所的价格冲击指数指标,计算出买卖双向的市场冲击成本。
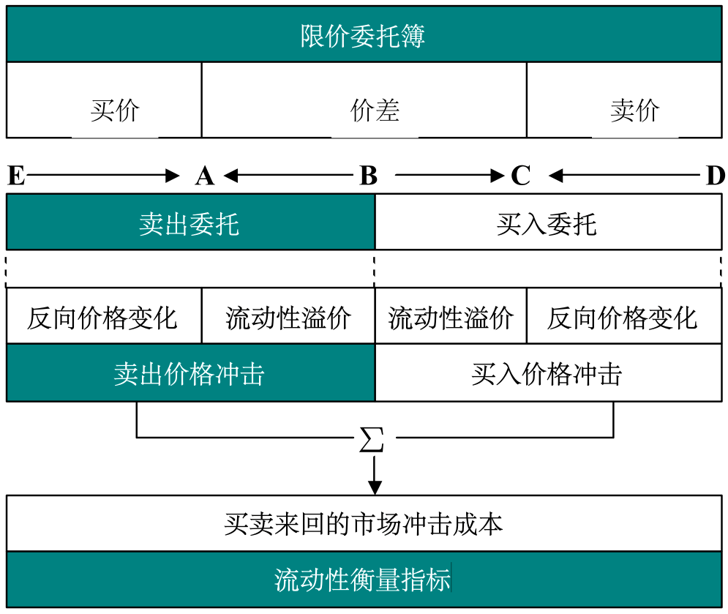
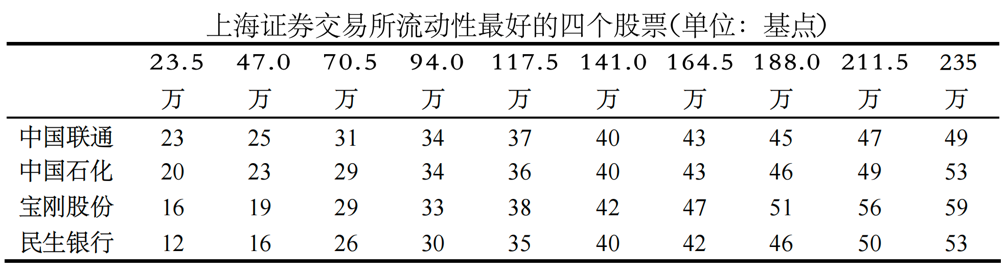
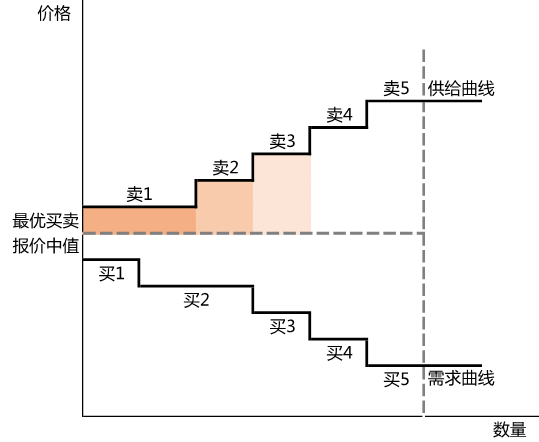
采用全市场股票的1分钟频快照(snapshot)数据构建出冲击成本因子。其中,买入冲击成本 = (购买一定金额股票的实际平均价格 − 最优买卖报价中值) / 最优买卖报价中值,卖出冲击成本 = (最优买卖报价中值 − 卖出一定金额股票的实际平均价格) / 最优买卖报价中值,总冲击成本 = 买入冲击成本 + 卖出冲击成本
下图展示了3种不同成交金额下,SH600000在2023-06-30的1分钟频日内(intra-day)冲击成本走势。可以看到,当成交金额越大时,冲击成本越高。
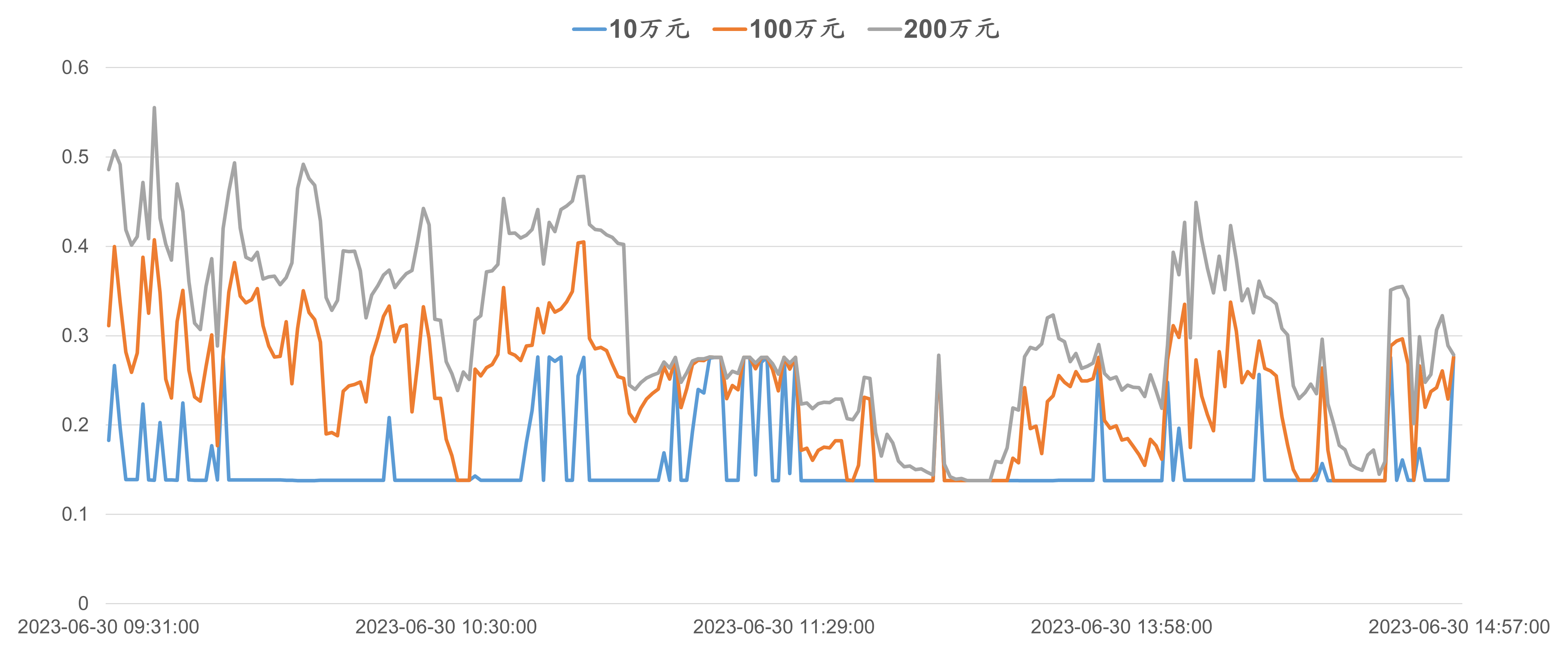
1.2 弹性因子
Harris (2003) 指出,弹性可以描述为价格在大量订单引起失衡之后,失衡价格恢复到其基本价格的速度。恢复速度越快,则弹性越好。本研究采用前序研究《弹性因子研究》中的方式构建弹性因子。下图展示了SH600000在2023-06-30的1分钟频收盘价(取自然对数后)分解及弹性。
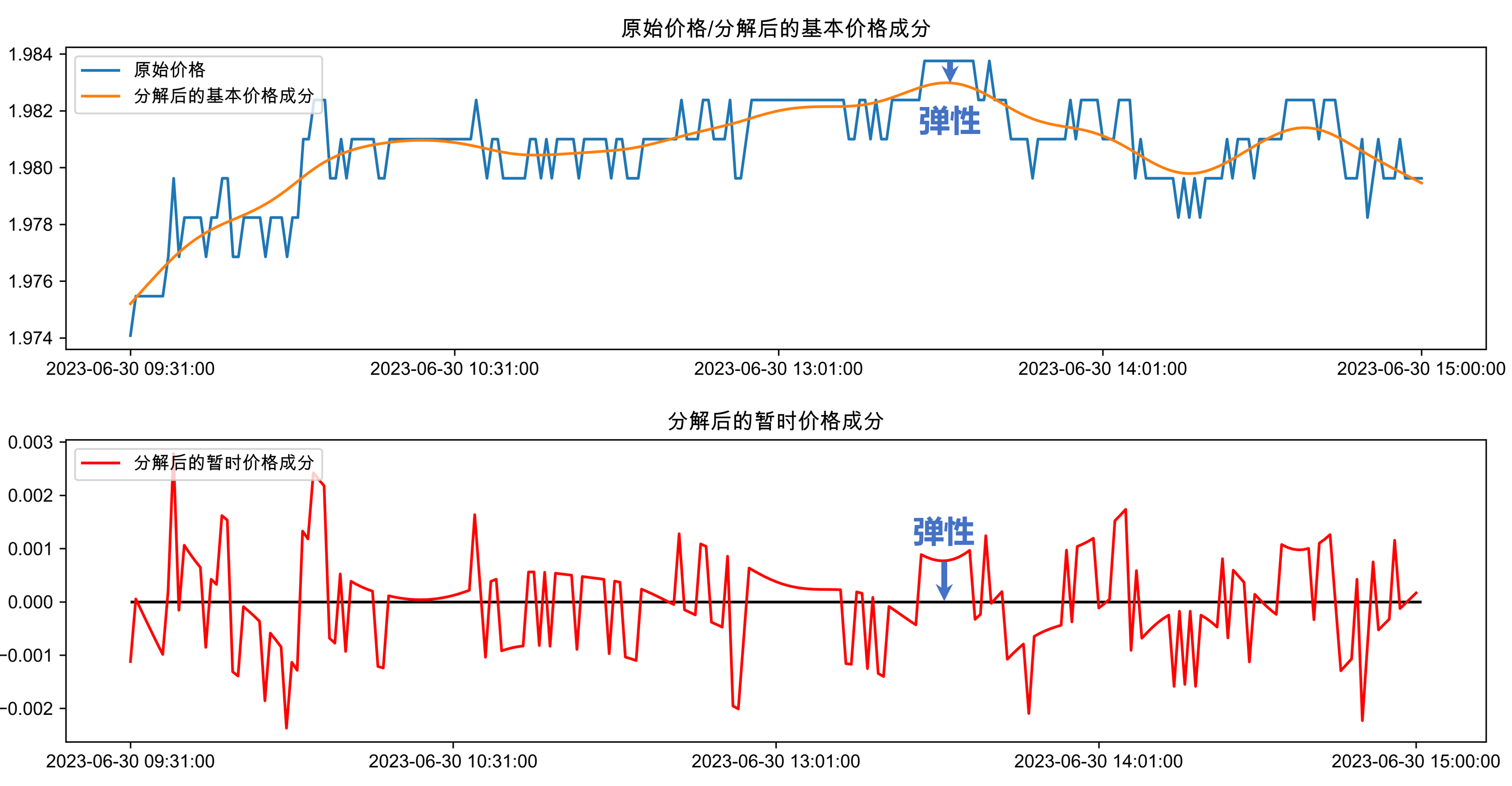
1.3 Amihud非流动性因子
该因子的定义为:在1分钟频率中,单位成交额驱动下,股价的变化幅度。变化幅度越小,则说明股票的流动性越好。
\[\begin{align*} Amihud\_illiq = \frac{1}{T-1} \sum^T_{t=2} \frac{|r_t|}{p_t \times v_t} \end{align*}\] 1.4 换手率因子换手率考量了股本的周转率情况;换手率越高,则在一定程度上股票的流动性越好。
\[\begin{align*} 换手率 = \frac{成交金额}{流通市值} \end{align*}\] 1.5 流动性综合打分总流动性因子由上述4个因子去量纲后等权构成:总流动性因子↑ = (-冲击成本因子↓) + 弹性因子↑ + (-Amihud非流动性因子↓) + 换手率因子↑
SH600000在2020-07-01~2023-06-30期间的流动性综合打分如下图所示:
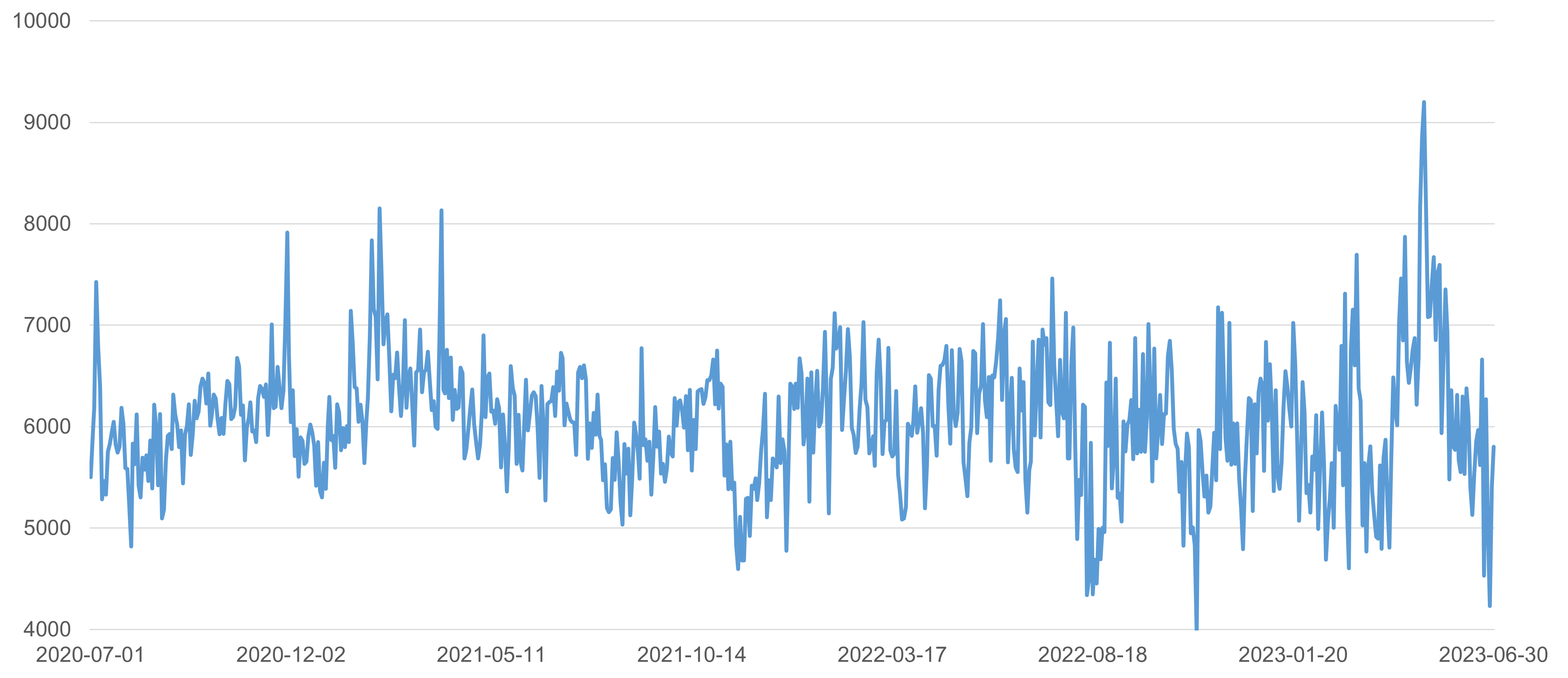
二、基于流动性走势的二元概率预测多日订单拆分算法
在得到上述流动性综合打分后,将其转化“当前流动性处于过去20个交易日的历史百分位”:
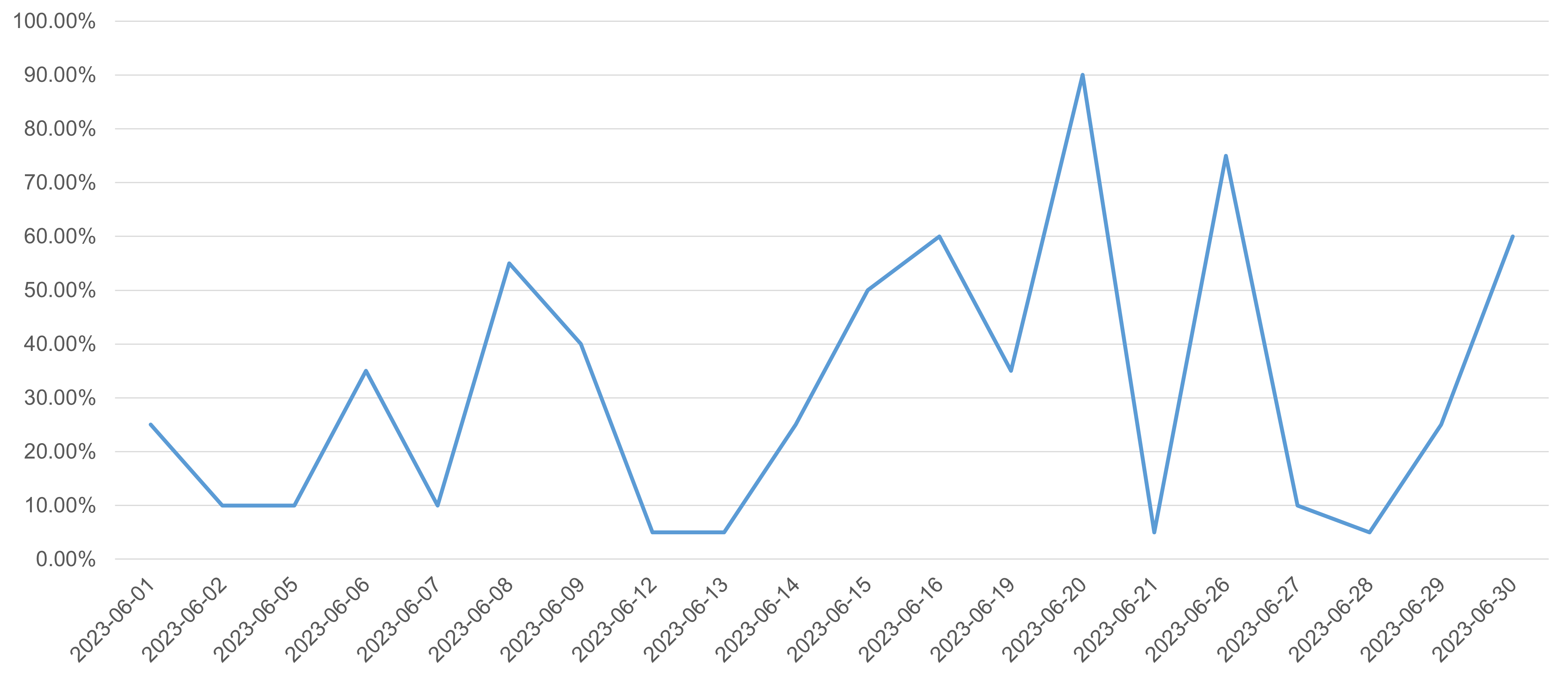
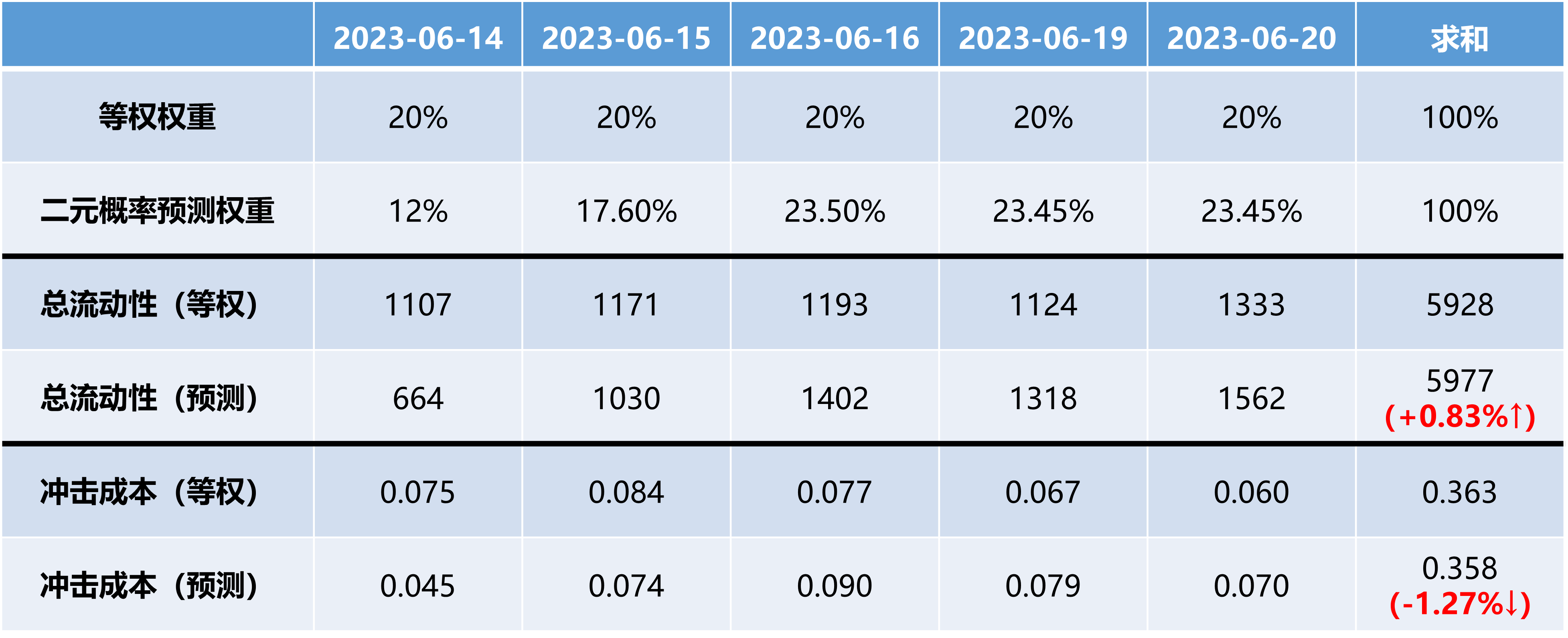
以下通过一个例子来对该多日订单拆分算法进行解释。在该例子中,假设2024-06-13为指令日,并在未来5个交易日即2024-06-14、2024-06-15、2024-06-16、2024-06-19、2024-06-20完成订单成交,该算法的目的在于将需要成交的总份额,合理分布于这5个交易日中,在流动性高的交易日成交更多的份额,在流动性低的交易日成交更少的份额,以此降低冲击成本,最终达到降低交易成本的目的。
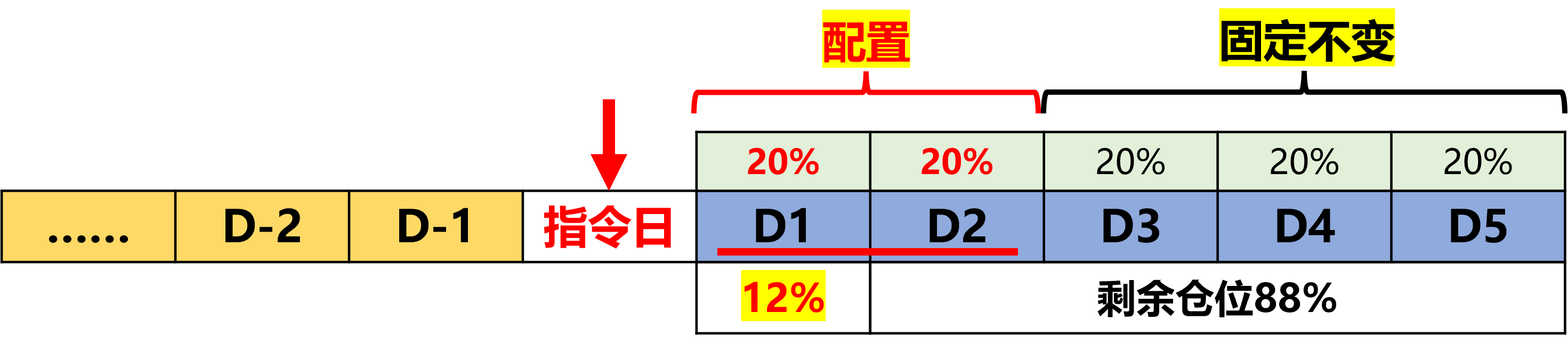
指令日(2023-06-13)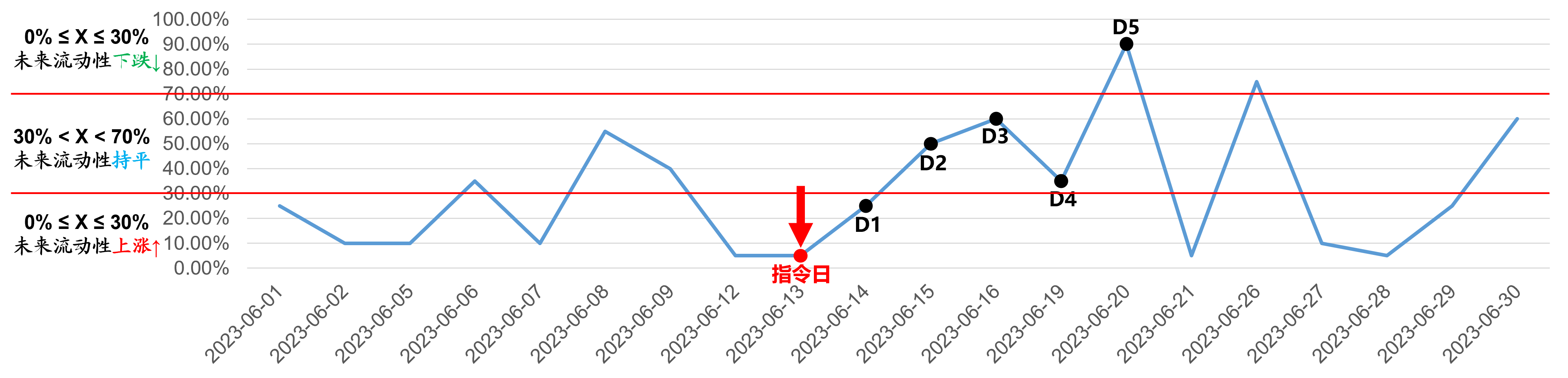
2、则未来第一天的交易仓位为:100% / 5 * 2 * 30% = 12%
3、剩余交易仓位为:100% – 12% = 88%
Day-1(2023-06-14)
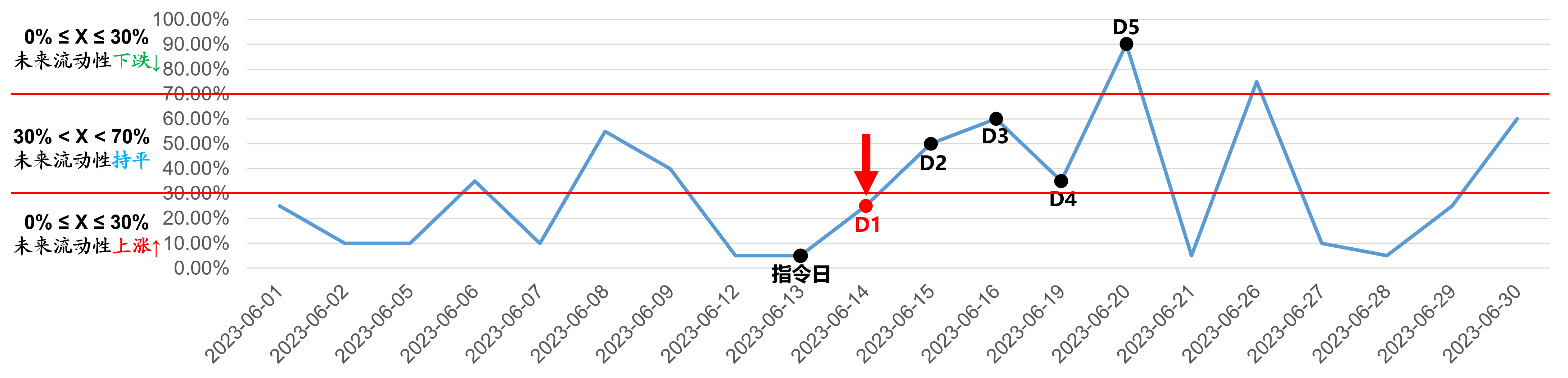
2、未来第一天的交易仓位为:88% / 4 * 2 * 40% = 17.6%
3、剩余交易仓位为 88% – 17.6% = 70.4%
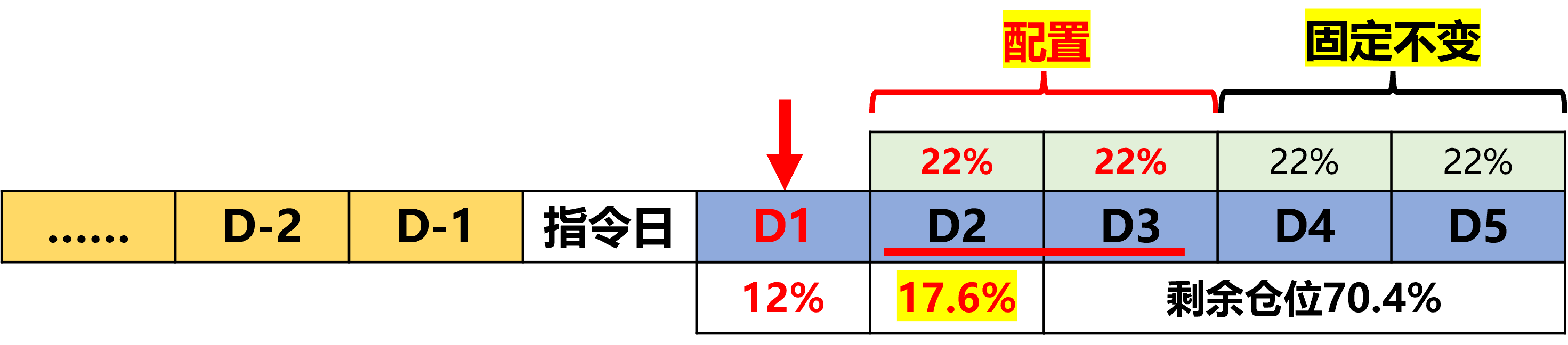
Day-2(2023-06-15)
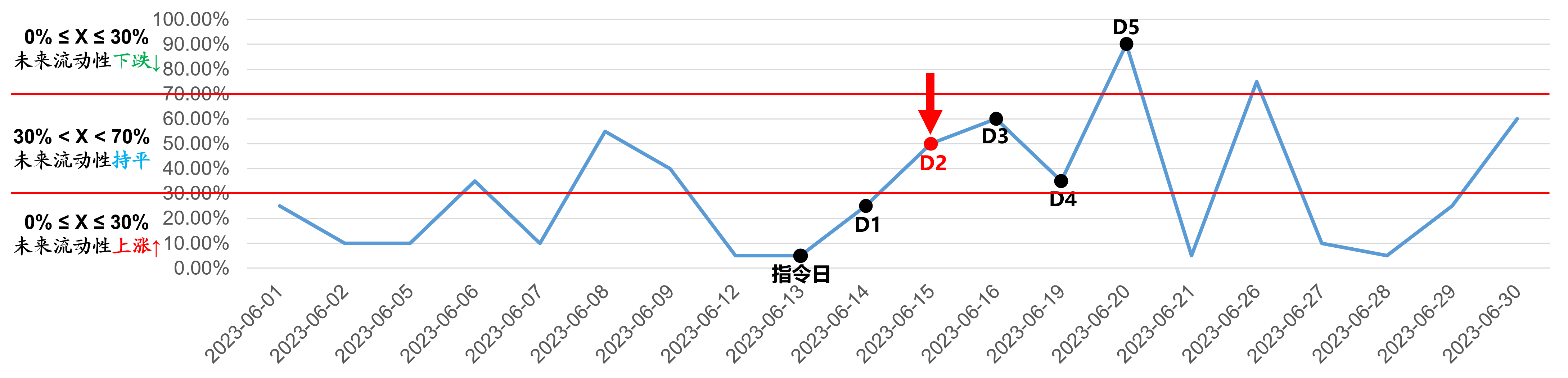
2、未来第一天的交易仓位为:70.4% / 3 * 2 * 50% = 23.5%
3、剩余交易仓位为 70.4% – 23.5% = 46.9%
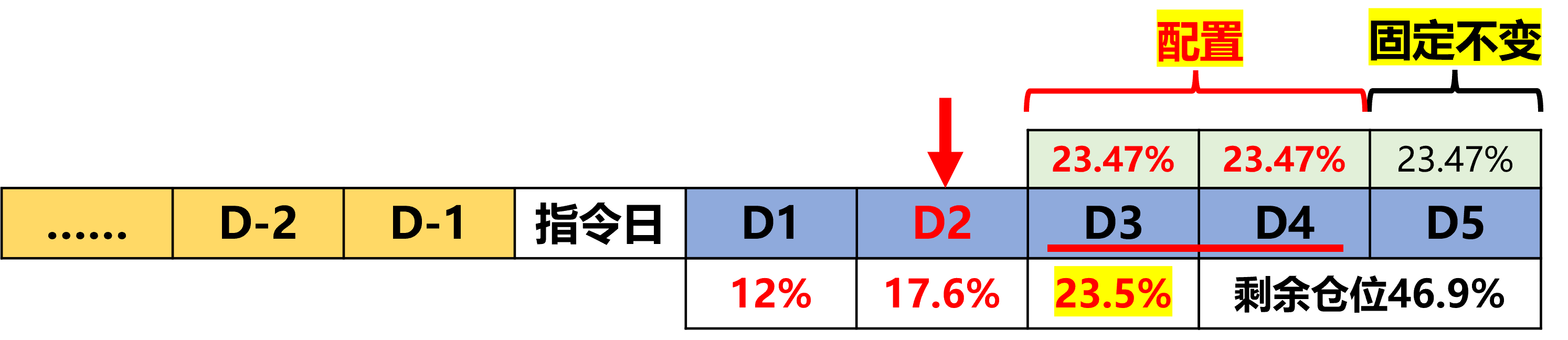
Day-3(2023-06-16)
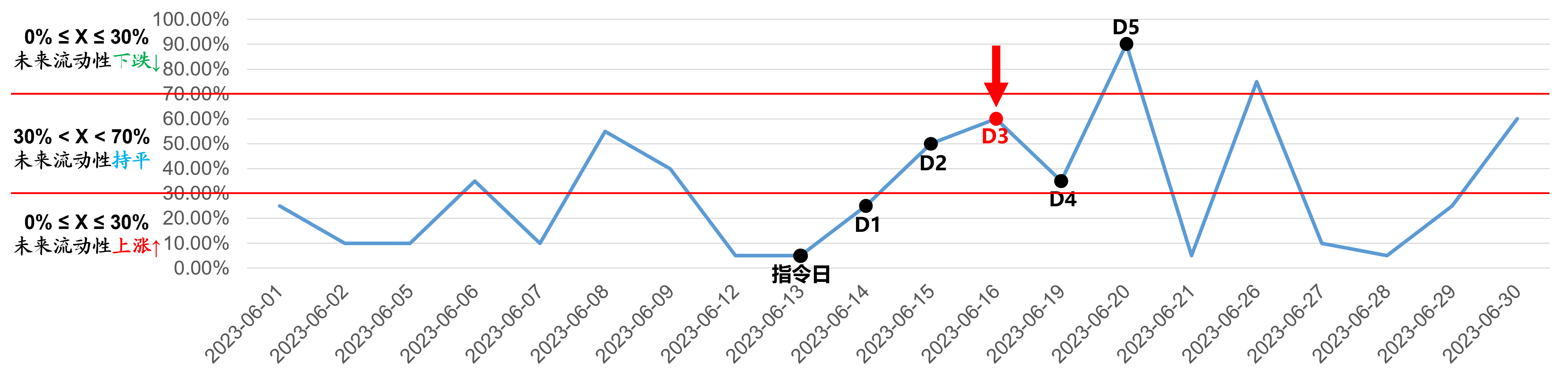
2、未来第一天的交易仓位为:46.9% / 2 * 2 * 50% = 23.45%
3、最后一日交易仓位为 46.9% – 23.24% = 23.45%
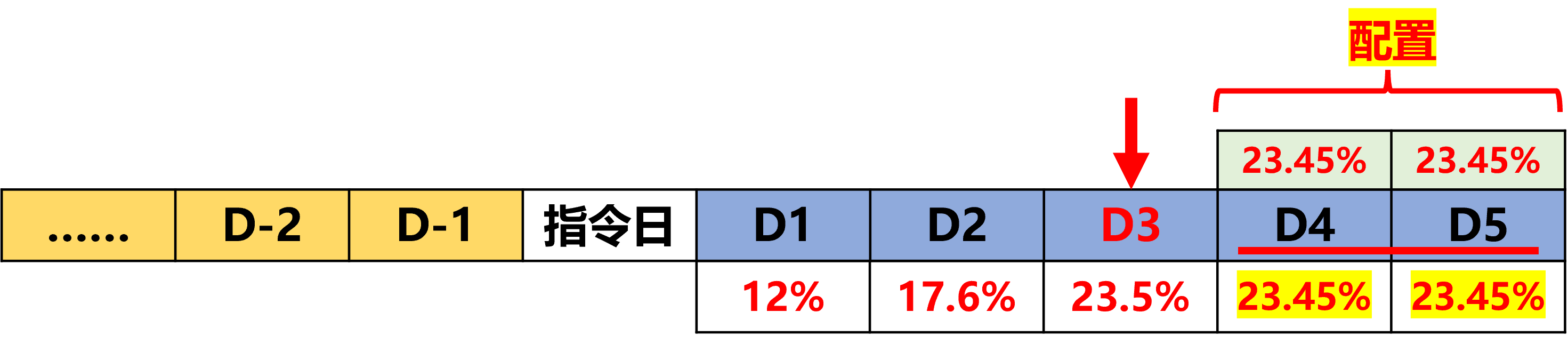
至此,基于流动性走势的二元概率预测多日订单拆分算法,已将总的交易份额拆分分配到5个交易日中。与等权策略相比,本研究提出的订单拆分策略能够更好地实现“在流动性高的时候交易更多份额”,从而有效较低交易成分:
三、基于冲击成本分布统计的日内订单拆分算法
在前文中,通过“基于流动性走势的二元概率预测多日订单拆分算法”,把总订单拆分为了多个单日订单。而本小节则进一步地根据个股的日内冲击成本分布统计,将单日订单拆分为分钟级订单甚至是秒级订单。
本日内订单拆分算法的核心思想在于:在日内冲击成本较低的时候赋予更大交易量,反之则赋予更小交易量。
以一个具体例子来对该算法进行解释。假设当前需要进行日内订单拆分的交易日为2023-07-03。首先对标的个股过去1个月(20个交易日,即2023-06-01~2023-06-30)的日内分钟频冲击成本进行指数加权统计,赋予近期更大、远期更小的权重,得到以下的日内分钟频冲击成本统计结果。
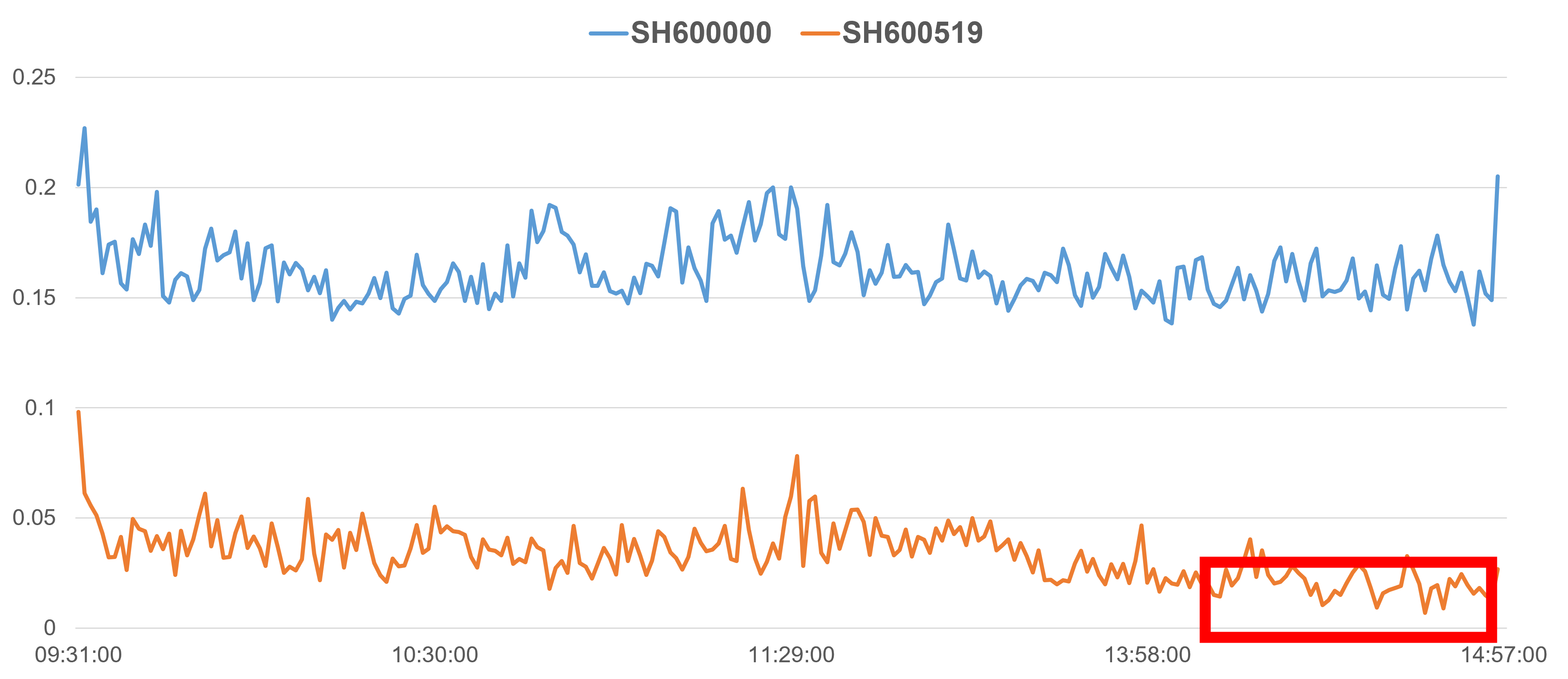
在上述例子中,SH600000的日内冲击成本分布较为平均,而SH600519在收盘前(上图中的红框时段)冲击成本相对较低。因此,在根据冲击成本把当日订单拆解为分钟频订单时,将在冲击成本较低的时段(下图中相应的红框时段),分配成交相对较多的份额。

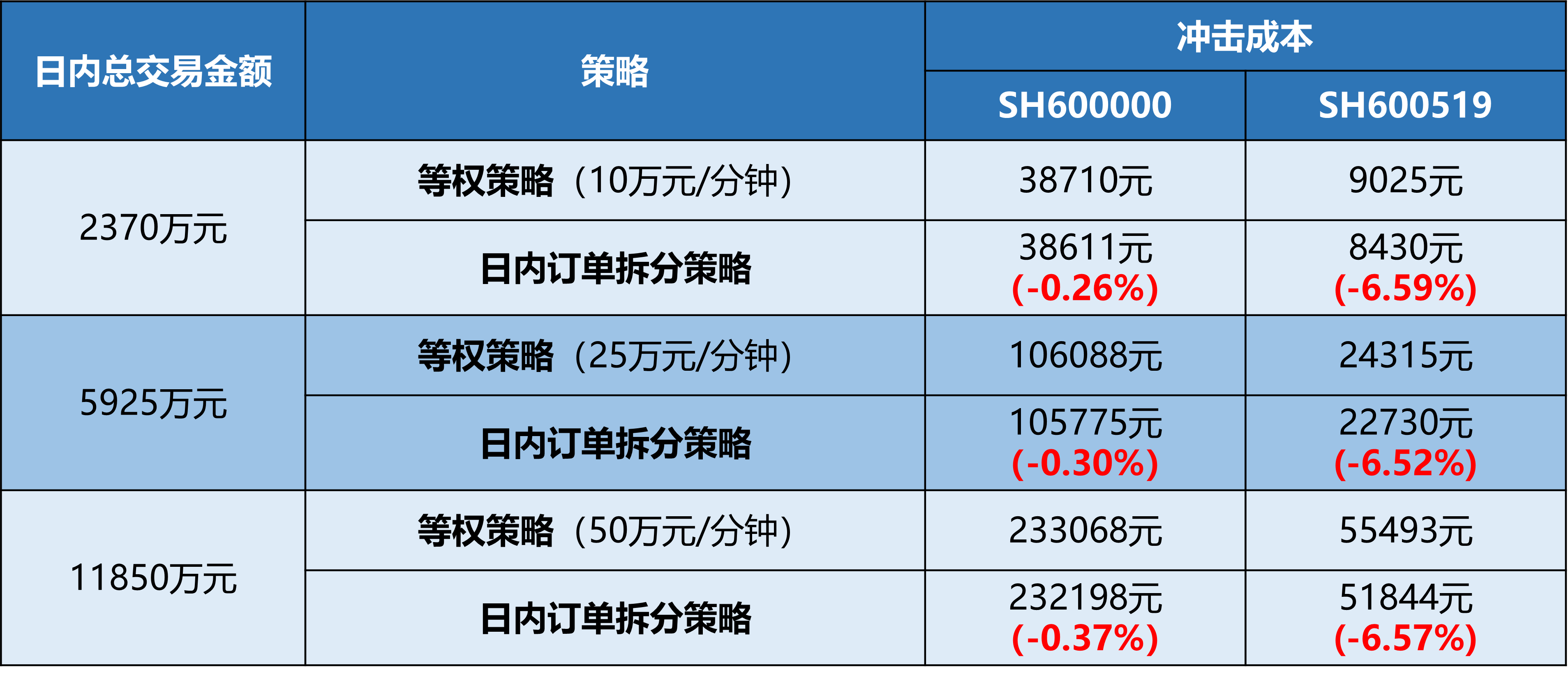
相对日内等权策略而言,基于冲击成本分布统计的日内订单拆分算法,在不同成交金额需求下都能够较为有效地较低交易成本。
四、综上所述,本订单策略的总体算法流程如下图所示:
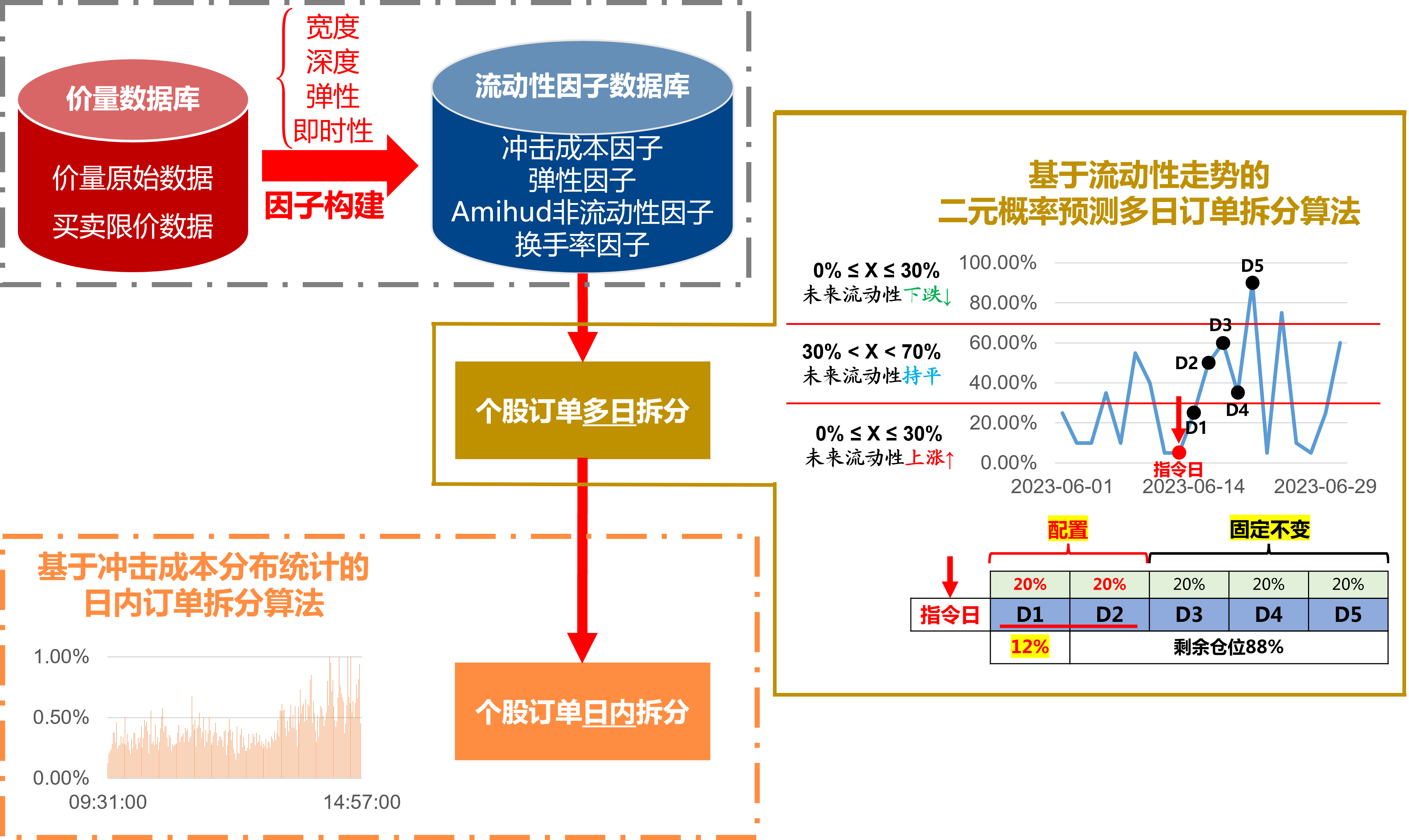
该算法存在以下几个优势:
4.1 风险分散1、每次决策影响的仓位分布是有限的;
2、基于每日最新行情数据进行多次决策;
3、拆分算法与预测模型相分离。在预测模型中,除了流动性,还可以加入其他考虑的因素,如股价走势。
4.2 模型简单、拓展性强
1、适用于2~N日的不同建仓周期;
2、二元概率预测,同时适用建仓和清仓;
3、可将拆解后的日内订单进行进一步分解。
五、总结与展望
本研究针对冲击成本所带来的额外交易成本,从流动性的角度进行分析,提出了从多日到日内的订单拆分算法。在该算法中,其核心思想为:在流动性高的时候交易更多的份额,而在流动性低的时候交易更少的份额。
而在股票的实际成交中,除了冲击成本外,还需要考量股票在买入时点的自身价格高低。因此,在订单拆分算法中,对股价的走势判断是另一个重要的考虑因素。
展望未来,可以在本研究算法模型中加入对股价走势的研判,综合考虑股票的“流动性+股价”,在价和量之间找到最佳平衡点,实现交易成本的全局最优。
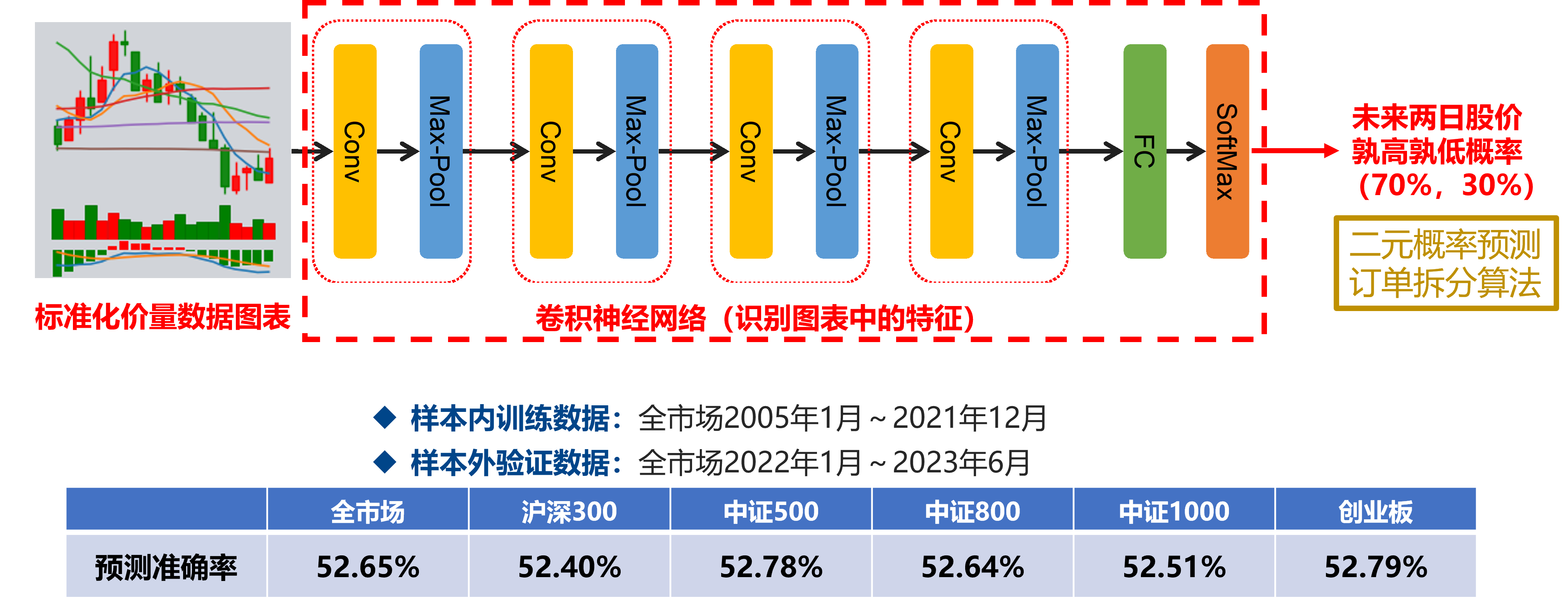
比如,可以结合前序研究《深度学习研究报告:基于卷积神经网络的股价走势AI识别与分类》中的股价预测模型,采用机器学习的方法来对股价的未来走势进行研判
参考文献(部分)
[1] 施东晖. 上海股市的流动性和市场冲击成本分析[M]. 上海证券交易所研究中心, 2006.
[2] Kim J, Kim Y. Transitory prices, resiliency, and the cross-section of stock returns[J]. International Review of Financial Analysis, 2019, 63: 243-256.